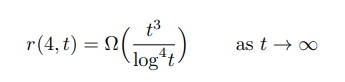How do you solve a mathematical problem that’s seen no progress in 40 years? Dr Sam Mattheus, affiliated with the Vrije Universiteit Brussel, went to the US for a year to find out. He combined his knowledge of finite geometry with traditional graph theory and not only solved a decades-old problem, but also offered an innovative alternative for the current approach to Ramsey problems. “Finite geometry can hopefully also offer solutions for calculating other Ramsey numbers,” says Mattheus.
The question Mattheus solved was a so-called Ramsey number. These are fundamental quantities that reflect the limits of possible disorder and are notoriously difficult to calculate. Yet Mattheus succeeded in just a few months, working with Prof Jacques Verstraete of the University of California San Diego (UCSD). “It was a big surprise for us,” he says. “For a long time, it wasn’t clear how we were going to approach it, or whether it would work at all.” One day, Mattheus went to Verstraete’s office with an idea. After a couple of hours of philosophising, they got to work. Just a few months later, they would find a solution for the specific Ramsey problem: r(4,t).
Mattheus obtained his PhD in finite geometry from VUB in 2022. He convinced the Belgian American Educational Foundation and the Fulbright scholarship programme to finance his research into Ramsey theory and left for the US with a plan. “I’d been walking around for years with the idea of using finite geometry to calculate Ramsey numbers,” he says. In the US, he’s currently working as a guest researcher at USCD under the supervision of Verstraete. This collaboration is no coincidence. “Prof Verstraete and Prof Dhruv Mubayi of the University of Illinois previously wrote a paper that inspired me to use a geometric perspective to solve one of the Ramsey questions.”
The idea was there, but the execution was still missing. Graph theory is the traditional way to calculate Ramsey numbers, Mattheus added his own knowledge. Using a Hermitian unital, a known object in finite geometry, he found the key to solving the problem r(4,t). “It was a question of combining two fields, finite geometry and graph theory,” says Mattheus. “The knowledge was there, but the ideas hadn’t been brought together, yet. It was all about the right place and the right time. In a way, we are actually advocating more cooperation within mathematics. Finite geometry can hopefully offer solutions for calculating other Ramsey numbers, as well.”
But how does it feel to solve a problem that’s decades old? “The reaction from the ‘graph theory community’ has been surreal. A day after we’d put the proof online, I got a phone call, asking if I could speak about the proof at a conference the following week. Soon, I’ll even be giving a lecture in China.” Mattheus only obtained his doctorate in 2022, but things are moving quickly. “When someone like Timothy Gowers tweeted about it and said he’d tried to solve the problem himself, it was quite a shock.” Gowers received the Fields Medal in 1998, known as the Nobel Prize for mathematicians under 40.
In October, Mattheus will return to the Department of Maths and Data Science at VUB with a grant from the FWO. “I’m looking forward to coming back to Brussels with a rucksack full of problems and working further on Ramsey theory with my colleagues.”
Ramsey theory
Ramsey problems relate to the time required for patterns to appear in disorder. They are part of combinatorics, where mathematicians look at sets of objects. An example of a Ramsey problem that is already solved is r(4, 5) = 25. Using the metaphor of a party with friends and strangers, in this case you would invite 25 people. According to the Ramsey number, this will create a group with four mutual acquaintances or a group with five strangers. To prevent these groupings, you can only invite 24 people. With 24 invitees, it would be possible to achieve a composition where there is no group with four acquaintances or five strangers. Mathematicians also use the terms red clique and blue clique to describe the two groups. The maximum number of invitees to avoid four mutual acquaintances (red clique) or six strangers (blue clique) is still unknown. Dr Mattheus fixed the red clique at 4 and examined what happened to the Ramsey number as the blue clique got bigger. In mathematical language, Mattheus and Verstraete’s result looks like this: